▶ 🎖 Problemas de relojes 🕑
¿Y si los relojes sirven para algo más que dar la hora? ¿Puede haber problemas de relojes interesantes? ¿Qué es mejor un reloj que no funciona o uno que se retrasa/adelanta 2 minutos al día?
En esta entrada vamos a hablar de relojes, pero de problemas que se pueden hacer con relojes. Es posible que hayas llegado aquí desde la página de problemas ariméticos o bien directamente después de leer otras entradas. Sea como sea hoy toca hablar de relojes.
No de estos no vamos a hablar. No son estos los problemas de relojes que vamos a estudiar
Efectivamente de estos son los relojes de los que vamos a hablar. Los problemas de relojes que estudiaremos son aquellos que se pueden plantear en relojes de manecillas
Introducción
Mi experiencia me dice que no todos los alumnos saben leer un reloj de manecillas 
Esta es la esfera de mi reloj:

Como puedes ver en este reloj hay varias cosas en las que fijarte:
- Una vuelta completa puede indicarte 60 s, 60 min o 12 h dependiendo de en qué manecilla te fijes, ya que se trata de un sistema sexagesimal. Vamos a ir viéndolas poco a poco.
- El reloj tiene 12 marcas principales (son las horas) y luego 60 marcas más pequeñas o secundarias (son los minutos). Así pues dos marcas principales comprenden una hora de tiempo, pero también marcan de cinco en cinco minutos.
- La manecilla azul, que no todos los relojes tienen, indica los segundos. Y se lee sobre las marcas secundarias. En esta fotografía está situada entre las marcas principales de 4 y 5 por lo tanto está señalando entre 20 y 25 segundos. Si te fijas está marcando el segundo 23.
- La manecilla verde es el minutero. Debemos leerla igual que el segundero, es decir, sobre las marcas secundarias. En este caso está entre las marcas principales 7 y 8, lo que nos indica que marca entre 35 y 40 minutos. Si te fijas un poco más, está marcando 38 minutos.
- La manecilla en rojo indica las horas. Se llama horario y se lee sobre las marcas principales. Así, en este caso indica pasadas las 12 pero antes de las 13 (esta foto está tomada por la mañana y no por la noche). Así pues aún no son las 13 horas pero ya ha pasado el mediodía.
- La hora que está marcando el reloj son las 12:38:23
- ¿Cómo sabes si es de noche o de día? Bueno, muchos relojes no te lo dicen, así que lo más fácil es mirar por la ventana
Y ahora que ya sabes cómo se lee un reloj estás listo para enferntarte a problemas de relojes. Sin embargo, antes responde a algunas preguntas:
- ¿Qué manecilla es la más lenta?
- ¿Cómo podrías medir la velocidad de las manecillas?
- ¿Cuántas veces se cruzan el minutero y el horario en 12 horas (es decir, en una vuelta completa del horario)?
Te dejo estas preguntas para que reflexiones sobre ellas, porque implícitamente las vamos a usar para resolver algunos problemas.
Problemas de relojes
A continuación te enumero varios problemas de relojes para que los intentes tú solo. Algunos de ellos los conozco desde hace muchos años como pasatiempos con las versiones que te propongo aquí u otras diferentes («La esfera del reloj»; «Los tres relojes»; «¿Cuándo se encuentran las manecillas?»; «¿Cuándo las manecillas están dirigidas en sentidos opuestos?»; «A ambos lados del 6») , pero todos los problemas que te sugiero los puedes encontrar en el libro de Yakob Perelmann (échale un 
- (La esfera del reloj) Más adelante puedes ver la esfera de un reloj. ¿Cómo te las puedes ingeniar para conseguir cortarla en seis (6) partes de manera que la suma de los números que hay en cada parte sea constante? Este problema tiene por objeto probar no tanto tu ingeniosidad como tu vivacidad.
- (Los tres relojes) Imagínate una casa donde hay tres relojes (lo cierto es que para este problema da igual que sean de manecillas o no). Imagínate, también, que a las 0:00:00 del uno de enero marcan todos la hora correcta; sin embargo sólo el primer reloj marcha bien. El segundo reloj se retrasa un minuto al día y el tercer reloj se adelanta otro minuto diario. ¿Cuándo volverán a dar la hora a la vez? ¿Será la hora exacta?
- (Los dos relojes) En mi casa tengo dos relojes: uno de pared y el despertador. Ayer los sincronicé. El reloj de pared se atrasa dos minutos por hora, mientras que mi despertador se adelanta un minuto cada hora. Cuando he vuelto a casa, he comprobado que ambos se habían parado y las manecillas marcaban: en el de pared las siete en punto, y en el despertador las 8 en punto. ¿A qué hora sincronicé ayer los relojes?
- (¿Cuándo se encuentran las manecillas?) A las 12 las manecillas del rel reloj están una sobre la otra, es decir, comprenden un ángulo de
 . ¿A qué horas vuelen a formar un ángulo nulo?
. ¿A qué horas vuelen a formar un ángulo nulo? - (¿Qué hora es?) -¿A dónde vas con tanta prisa?
-Al tren de las seis. ¿Cuántos minutos quedan hasta su salida?
-Hace 50 minutos quedaban 4 veces más minutos después de las tres.
¿Qué significa esta rara respuesta? ¿Qué hora era? - (A ambos lados de las seis) Ayer por la tarde miré mi reloj y vi que ambas manecillas estaban a ambos lados dela cifra 6, formando el mismo ángulo. ¿A qué hora fue esto?
- (¿Cuándo están las manecillas dirigidas en sentidos opuestos?) A las 6 sucede lo contrario que a las 12, las manecillas están dirigidas en sentidos opuestos y forman un ángulo llano. ¿Cuándo vuelve a ocurrir esto después de las
 ?
? - (¿A qué hora?) ¿A qué hora adelanta el minutero al horario la misma distancia exactamente que éste se halla por delante de la cifra 12 en la esfera? ¿Puede ocurrir esto en varios instantes durante el día, o no ocurre nunca?
- (Al contrario) Es posible que hayas observado una situación contraria, es decir, donde el horario y el minutero están a ambos lados del número 12, ambos a la misma distancia del número y el horario delante. ¿Cuándo ocurre eso?
- (Tres y siete) Un reloj da las tres. Mientras suenan las campanadas pasan 3 segundos. ¿Cuánto tiempo será necesario para que este reloj dé las siete? Por si acaso, te prevengo que no se trata de un problema de broma y que no encierra ninguna trampa.
- (El tictac del reloj) Este es un problema más de fisiología que de matemáticas, pero la Finalmente, haga el pequeño experimento siguiente. Ponga su reloj sobre la mesa, aléjese de él tres o cuatro pasos y escuche su tictac. Si en la habitación reina un silencio suficiente, escuchará usted que su reloj parece que marcha con interrupciones: el tictac se oye durante cierto tiempo, luego deja de oírse varios segundos, vuelve otra vez a sonar y así sucesivamente. ¿Cómo se explica esta marcha irregular?

Cómo identificar los problemas de relojes
Los problemas de relojes se indentifican muy facilmente porque el propio enunciado te lo dice. Te vas a encontrar cuestiones del estilo ¿En qué momento las manecillas de un reloj…? o bien ¿Cuándo se cumple que en un reloj… ?
¿No te crees el párrafo anterior? Pues échale un vistazo a los enunciados de los problemas que te he propuesto…
Cómo enfrentarte a los problemas de relojes
Depende del problema, pues de los que te he dejado escritos arriba algunos se resuelven de una manera y otros de otra. No obstante, algunas veces podrás interpretar un problema de relojes como un problema de persecución, donde el horario debe alcanzar o quedarse a determinada distancia de minutero o al revés.
Por tanto es muy importante que sepas las velocidades de cada aguja.
- La velocidad del horario es de una vuelta cada 12 horas, es decir
 o si lo prefieres en radianes:
o si lo prefieres en radianes: 
- La velocidad del minutero es mucho mayor, ya que da una vuelta cada hora, es decir
 y en radianes
y en radianes 
- El segundero claramente es el más veloz de todos, así que su velocidad será

Como ves te he puesto todas las velocidades en las mismas unidades para que podamos empezar a trabajar.
Resolución de los problemas de relojes propuestos
A continuación te voy a resolver todos y cada uno de los problemas anteriores. Te debo decir que los he clasificado en tres categorías diferentes según creo que encajan mejor (como toda clasificación, es subjetiva, así que puede que no estés de acuerdo):
¡¡¡Vamos allá!!!
Problemas de relojes estándard
Estos problemas de relojes son aquellos que no requieren fijarse en particularidades de los mismos, si no tan sólo comprender bien el problema.
Los tres relojes
Imagínate una casa donde hay tres relojes (lo cierto es que para este problema da igual que sean de manecillas o no). Imagínate, también, que a las 12:00 del uno de enero marcan todos la hora correcta; sin embargo sólo el primer reloj marcha bien. El segundo reloj se retrasa un minuto al día y el tercer reloj se adelanta otro minuto diario. ¿Cuándo volverán a dar la hora a la vez? ¿Será la hora exacta?
Quizá lo más sencillo sea ver qué va ocurriendo con cada reloj y cada día a las ![]() . Para ello tenemos esta tabla:
. Para ello tenemos esta tabla:
| Reloj | 1-ene | 2-ene | 3-ene | 4-ene | 5-ene | 6-ene |
| A (correcto) | ||||||
| B (se retrasa) | ||||||
| C (se adelanta) |
Como ves cada 60 días el reloj B se habrá adelantado 1 hora y el reloj C se habrá retrasado otra tanto. Así que lo que ocurre en el reloj B es lo mismo que lo que ocurre en el reloj C pero uno hacia adelante y otro hacia atrás.
Así la pregunta que te debes hacer es: los relojes B y C se deben mover un total de 12 horas, lo que supone 720 minutos. ¿Cuántos días son? Y la pregunta es sencilla de responder: 720 días.
¿Qué hora es?
-¿A dónde vas con tanta prisa?
-Al tren de las seis. ¿Cuántos minutos quedan hasta su salida?
-Hace 50 minutos quedaban 4 veces más minutos después de las tres.
¿Qué significa esta rara respuesta? ¿Qué hora era?
Esto parece un trabalenguas y realmente parece que está hecho todo para despistar. Pero vamos a ir diseccionando el problema:
- El tren sale a las seis, luego son antes de las seis.
- Ya han pasado las tres, porque si no no tiene sentido la penúltima línea; luego son después de las tres.
Ya tenemos un marco temporal de 3 horas. como nos habla de minutos eso son 180 minutos.
La clave está en la penúltima línea (¿no podías haberle dicho la hora y ya está?, ¿no ves que lleva prisa?). Cuando te dicen que hace 50 minutos quedaban… significa «todo lo que te voy a contar es cierto si quitas 50 minutos a tu intervalo de tiempo» o dicho de otra manera, no vas a trabajar con 180 minutos sino con 180-50=130 minutos.
Y ahora repartimos esos 130 minutos. Date cuenta que tienes cuatro partes antes y una parte después; es decir, que tienes que repartir 130 en 5 partes iguales. Por lo que tienes que cada parte son ![]() .
.
Y ya está casi resuelto: Faltan 26 minutos para que salga el tren.
O no… porque ¿Y todo el galimatías que nos ha contado? Bien, si son las 17:34, hace 50 minutos eran las 16:44, y eso significa que habían pasado 1:44 desde las 15:00, es decir 104 minutos.
Y ahora viene la gracia. ¿Qué relación hay entre 104 y 26? Pues claramente ![]() , es decir la solución es correcta.
, es decir la solución es correcta.
Son las 17:34 y quedan 26 minutos para que salga el tren.
Tres y siete
Un reloj da las tres. Mientras suenan las campanadas pasan 3 segundos. ¿Cuánto tiempo será necesario para que este reloj dé las siete? Por si acaso, te prevengo que no se trata de un problema de broma y que no encierra ninguna trampa.
Aquí el truco está en cortar el tiempo. Me explico. Si dibujas lo que ocurre, y suponiendo que las campanadas estén equiespaciadas tienes lo siguiente:

Si durante las tres campanadas necesito 3 segundos, lo que ocurre es que la primera campanada se ha producido en el segundo 0, la tercera en el segundo 3. ¿Y cuándo se ha producido la segunda? ¿en el primer segundo? ¿en el segundo segundo?….
No. nada de eso. La segunda campanada se produce en el segundo ![]() . Es decir, has dividido el tiempo en dos partes.
. Es decir, has dividido el tiempo en dos partes.
Así pues, si necesitas siete campanudas, ¿En cuántas partes divides el tiempo?…. 
Ya lo has pensado….
Seguro que no estás haciendo trampa…
Efectivamente, ya sabes que el tiempo lo has dividido en 6 partes, y como cada campanada necesita 1,5\ s, eso da como resultado que necesitas 6 intervalos de 1,5\ s. O lo que es lo mismo 9 segundos.

Problemas que se resuelven como una persecución
Los problemas que hemos hecho en el apartado anterior eran estándar, es decir, aquellos que se pueden resolver tan sólo con pensar un poco cómo funciona un reloj y poco más.
Los problemas de relojes que vamos a resolver ahora se pueden plantear siempre como una persecución entre una aguja y la otra. Quizá el más típico sea el de cuándo se vuelven a encontrar las manecillas de un reloj (el primero), pero lo cierto es que cualquiera de ellos son variaciones más o menos directas del resto.
¿Cuándo se encuentran las manecillas?
A las 12 las manecillas del reloj están una sobre otra. Pero te habrás dado cuenta, probablemente, de que éste no es el único instante en que las manecillas se encuentran: durante el día alcanza la una a la otra varias veces. ¿Puedes decir todos aquellos instantes en que esto ocurre?
Cuando planteo este problema en clase, la respuesta que siempre oigo es ¡¡las 13:05!! pero es muy fácil hacer ver a los alumnos que esa hora no puede ser pues cuando el minutero ha llegado a los 5 minutos, el horario se ha ido de allí. Poco o mucho, pero lo cierto es que la manecilla del horario ya no está.
Me gusta en ese momento acotar un poco el problema. Porque esto nos obliga a pensar. Ya sabemos que tiene que ser después de las 13:05, pero ¿puedes asegurar que el cruce se tenga que producir antes de una hora determinada?… 
Así que ya sabemos mucho, sin haber hecho ninguna cuenta: sabemos que es un momento entre las 13:05 y las 13:10. Vamos a ver ahora si somos capaces de calcularlo y coincide con lo que, de momento, sabemos.
Lo que vamos a hacer es plantearnos el problema como si fuera una persecución entre la manecilla del horario que va delante y el a manecilla del minutero que va detrás, tal y como puede ver en el siguiente dibujo.

Todos los datos que necesitamos los podemos ver resumidos en la siguiente tabla:
| horario | minutero | |
| velocidad (º/h) | 30 | 360 |
| espacio (º) | s-30 | s |
| tiempo (h) | t | t |
Las velocidades anteriores te las he caclucado al inicio de esta sección por lo que no volveré a contártelo. Por otro lado imagínate la situación de las agujas a las 13:00 la separación entre ellas es un ángulo de 30º. ¡¡ahora empieza la persecución!! y te debes preguntar lo siguietne:
- ¿Cuánto tiempo están persiguiéndose? pues será el mismo tiempo para ambas manecillas. ¡¡Que el tiempo para ambos sea común es la clave del problema!!
- ¿Qué espacio recorren cada una? En este caso, el minutero recorre 30º más que el horario o bien, como te he puesto en la tabla, el horario recorre 30º menos que el minutero.
Y puesto que, teniendo el espacio y la velocidad, puedo calcular el tiempo con la siguiente fórmula: ![]() y debido a que ambos tiempos son iguales, puedo plantear la siguiente ecuación:
y debido a que ambos tiempos son iguales, puedo plantear la siguiente ecuación:
![]()
Y resolver esta ecuación de primer grado es trivial. Su solución es:
![]()
¿Y esto qué es? pues es el espacio que recorre el minutero, que no nos interesa porque no nos lo piden. TAn sólo nos interesa para que nos sirva para calcular el tiempo, que esto sí es lo que nos preguntan.
¿Y cómo calculo el tiempo? Pues con los datos del minutero:
![]()
Es decir, que desde las 13:00, las agujas tardan ![]() de hora en encontrarse; o lo que es lo mismo 0:5:27,27 Así pues:
de hora en encontrarse; o lo que es lo mismo 0:5:27,27 Así pues:
Se vuelven a encontrar a las 13:05:27,27
¿Cuándo están las manecillas dirigidas en sentidos opuestos?
A las 6 sucede lo contrario que a las 12, las manecillas están dirigidas en sentidos opuestos. Pero, ¿ocurre esto sólo a las 6, o hay otros instantes en que las manecillas se sitúan también así?
Este problema es una variación del anterior, y el resultado será muy parecido, como verás a continuación. Durante toda la hora de las 6 las manecillas no están en sentidos opuestos nunca. Así que podemos empezar la persecución a las 7:00 porque a esta hora conocemos la posición exacta de cada aguja.
La ventaja que tiene el horario respecto del minutero es de 210º grados tal y como ves en el siguiente dibujo

Y las manecillas estárán orientadas en sentidos opuestos cuando su distancia sea de 180º (30º menos) así que ya sabemos qué es lo que setamos buscando, y vamos a plantear la misma tabla que antes:
| horario | minutero | |
| velocidad (º/h) | 30 | 360 |
| espacio (º) | s | s+30 |
| tiempo (h) | t | t |
Si te das cuenta, los tiempos son iguales, y el tiempo es :![]() por lo tanto tenemos que:
por lo tanto tenemos que:
![]()
Y resolviendo esta ecuación obtenemos que ![]() Dos consideraciones:
Dos consideraciones:
- Este espacio es un cierto ángulo.
- No es necesario calcularlo, porque lo que pide el problema es untiempo, y esto es un ángulo.
Entonces ¿qué hacemos ahora? Fácil, calcular cuánto tiempo tarda una de las manecillas en recorrer ese espacio. Por ejemplo el horario:
![]()
Y esto sí nos interesa traducirlo a horas minutos y segundos. Al final, las manecillas están en sentidos opuestos a las:
![]()
A ambos lados de las seis
Yo miré el reloj y vi que sus dos manecillas estaban a ambos lados de la cifra 6 y a distancias iguales. ¿A qué hora fue esto?
En este caso tenemos dos posibilidades: que el horario vaya por delante; o bien que el minutero vaya por delante. Te lo muestro a continuación:
CASO 1: El horario va por delante del minutero
En este caso podemos decir que son algo menos de las 6:30, pero no tanto como las 6:25, pues si eso fuese el caso, la manecilla horaria estaría en las 7, lo cual no puede ser. Aunque parezca poco, ya hemos acotado la hora que debe ser.
Fíjate en el siguiente dibujo. Como ya sabemos que debe ser una hora entre las 6:25 y las 6:30, vamos a estudiar la posición de las agujas a las 6:25 porque sabemos exactamente cómo están colocadas:
Hallando una ecuación

- El minutero está colocado en la marca de 25 minutos, es decir forma un ángulo de 150º con la posición de las 12:00
- El horario estará colocado un poco después de la marca de las 6 horas ¿Cuánto después? pues tanto como haya recorrido en 25 minutos, que son
 Lo cual significa que forma un ángulo de
Lo cual significa que forma un ángulo de  con la marca de las 12:00
con la marca de las 12:00
Todo lo anterior lo puedes ver en la siguiente figura:

A partir de este momento, las manecillas de reloj se mueven un determinado ángulo. Vamos a llamar ![]() al ángulo que se mueve el horario, mientras que llamaremos
al ángulo que se mueve el horario, mientras que llamaremos ![]() el ángulo que se mueve el minutero. Estos dos ángulos no son los que nos pide el problema si no sólo lo que se mueven las agujas.
el ángulo que se mueve el minutero. Estos dos ángulos no son los que nos pide el problema si no sólo lo que se mueven las agujas.

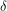 grados y el horario se mueve
grados y el horario se mueve 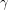 grados.
grados.Lo que sí puedes decir es que llegará un momento en que el minutero estará, en grados sexagesimales, tan cerca de la marca de los 30 minutos, como lejos estará el horario de la misma marca. O dicho de otro modo:
- Cuán cerca está el minutero:
 Recuerda que cuando llegue a la marca de 30 minutos, el minutero formará un ángulo de 180º con la marca de las 12:00
Recuerda que cuando llegue a la marca de 30 minutos, el minutero formará un ángulo de 180º con la marca de las 12:00 - Cuán lejos estará el horario:
 porque esta aguja se habrá alejado desde su posición a las 6:25
porque esta aguja se habrá alejado desde su posición a las 6:25
Y lo que debe ocurrir es que ambos ángulos sean iguales:
![]()
Hallando otra ecuación
Pero con lo que hemos hecho hasta ahora sólo tenemos una ecuación con dos incógnitas. Nos falta otra ecuación. ¿De dónde la conseguimos? De las velocidades de las agujas.
![]()
Hay muchas opciones de cómo proceder a partir de ahora, pero yo lo que voy a hacer es dividir ambas ecuaciones. Esto lo puedo hacer por que sé que ni ![]() , ni
, ni ![]() ni
ni ![]() serán 0. Así obtengo:
serán 0. Así obtengo:
![]()
Hallando la solución
Ahora puedo plantear un sistema de dos ecuaciones con dos incógnitas:
![Rendered by QuickLaTeX.com \[\left.\begin{aligned} \delta&=17.5-\gamma\\ -\delta&=-\frac{1}{12}\gamma\end{aligned}\right\}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-da7accd39e4c3c76f0e3cd69386462bf_l3.png)
Y este sistema de ecuaciones tiene por solución:
![]()
![]()
Y sólo tenemos ahora que calcular cuánto tiempo tarda una de las agujas en recorrer ese ángulo. Sea, por ejemplo, el horario que tiene la velocidad más lenta. Tarda en recorrer ![]()
![]()
O lo que es lo mismo, ambas agujas formarán el mismo ángulo a las ![]()
CASO 2: El minutero va por delante del horario
En el caso de que el horario vaya por detrás la forma de resolución es la misma, pero partimos de los ángulos que tenemos a las 5:30 con respecto a la marca de las 12:00
- El minutero marca un ángulo de 180º con las 12:00
- El horario marca un ángulo de 165º con las 12:00 (¿puedes justificar por qué es así?)
A partir de ahora el horario recorrerá un ángulo ![]() desde su posición, mientras que el horario recorrerá un ángulo
desde su posición, mientras que el horario recorrerá un ángulo ![]() desde la suya. Llegará un momento en que el ángulo con la marca de los 30 minutos sea el mismo. Es decir, ocurrirá:
desde la suya. Llegará un momento en que el ángulo con la marca de los 30 minutos sea el mismo. Es decir, ocurrirá:
![]()
Y teniendo en cuenta, como antes, las velocidades de ambas agujas obtenemos el siguiente sistema de ecuaciones:
![Rendered by QuickLaTeX.com \[\left.\begin{aligned} \alpha&=15-\beta\\ -\alpha&=-\frac{1}{12}\beta\end{aligned}\right\}\]](https://www.cursomates.com/wp-content/ql-cache/quicklatex.com-42ccc012fb87c3e09b68aaa974bfb1c8_l3.png)
Cuyas soluciones son
![]()
![]()
Ahora tomemos una de las velocidades de las agujas y hallemos cuánto tiempo tarda en recorrer essa distantaicia. Por ejemplo, el minutoer:
![]()
Es decir, la hora a la que esto ocurre son las 5:27:18.46.
Al contrario
Si has seguido con atención la marcha de un reloj es posible que hayas observado precisamente una posición de las manecillas contraria a la que acabamos de mencionar, es decir, la posición en que el horario adelanta al minutero en tanto como este último ha pasado del número 12. ¿Cuándo ocurre esto?
Este problema no es más que una variación de los dos anteriores. En este caso, la hora de partida es la 1:00

A partir de ahora te debes hacer las siguientes preguntas:
- ¿Qué ángulo forman ambas agujas? Esta es fácil 30º
- Cuando comiencen a moverse las agujas…
- ¿Qué distancia (ángulo) recorrerá el minutero? Sea
 .
. - ¿Y el horario? Sea
 .
.
- ¿Qué distancia (ángulo) recorrerá el minutero? Sea
- En algún momento el ángulo entre las 12:00 y el minutero será igual que entre el minutero y el horario. Es decir:
![]()
Te explico qué significa esta ecuación:
 es el ángulo que hay entre ambas agujas: partimos de 30º, le sumamos lo que recorre el horario,
es el ángulo que hay entre ambas agujas: partimos de 30º, le sumamos lo que recorre el horario,  , y le restamos lo que recorre el minutero
, y le restamos lo que recorre el minutero  .
.- Lo anterior debe ser igual al ángulo recorrido por el minutero,
 .
.
Pero ahora necesitamos otra ecuación, porque de momento sólo tenemos una ecuación con dos incógnitas. ¿De dónde las sacamos? De las velocidades, igual que antes. Al final vas a poder plantear el siguiente sistema:
![]()
Sus soluciones son:
![]()
![]()
Pero como de costumbre nos piden un tiempo. Vamos a calcularlo:
![]()
Es decir que lo planteado en el problema ocurre a las ![]()
Si quieres puedes dejarme en comentarios a qué otras horas del día ocurre esto, hay unas pocas.
¿A qué hora?
¿A qué hora adelanta el minutero al horario en la misma distancia exactamente que éste se halla por delante de la cifra 12 en la esfera? ¿Puede ocurrir esto en varios instantes durante el día, o no ocurre nunca?
En este caso vamos a partir de las 12:00 En ese momento la situación de las manecillas es la que ves en el siguiente figura:

¿Qué ocurre ahora? pues que se empiezan a mover. Si llamamos ![]() al ángulo que avanza el horario, y
al ángulo que avanza el horario, y ![]() el ángulo que avanza el minutero; siempre respecto de la marca de las 12:00 Las condiciones del problema se verifican cuando:
el ángulo que avanza el minutero; siempre respecto de la marca de las 12:00 Las condiciones del problema se verifican cuando:
![]()
Y teniendo en cuenta las velocidades, habrá que resolver la siguiente ecuación:
![]()
Y su resolución es muy sencilla. Si operas obtienes que el momento en que esto ocurre es ![]()

Efectivamente la respuesta es correcta. Si partimos de las 12:00, la situación que nos pide el problema nunca llega a ocurrir, pues que para cualquier espacio que recorra el minutero (y ya sabes que aquí espacio significa ángulo); el horario recorrerá ![]() Así que entre las 12:00 y la 1:00 puedes estar seguro que no ocurre ninguna vez lo que plantea el problema.
Así que entre las 12:00 y la 1:00 puedes estar seguro que no ocurre ninguna vez lo que plantea el problema.
¿Podrías calcular cuando ocurre por primera vez la situación descrita en comentarios? Puedes dejarlo en comentarios, si deseas.
Problemas de ingenio
Para la resolución de estos problemas hace falta que se ilumine una bombilla 
La esfera del reloj
La esfera de este reloj (puedes ver más abajo una figura, puedes descargártela e imprimirla) debe cortarse en seis partes de forma cualquiera, de modo que la suma de los números que haya en cada parte sea la misma. Este problema tiene por objeto probar no tanto tu ingeniosidad como tu vivacidad.

Fuente: www.librosmaravillosos.com
De momento no te voy a resolver este problema. Lo dejaré y esperaré a que en comentarios vayan apareciendo diferentes soluciones. De momento te doy una pista: ¿Cuánto sumarán los números en cada sección en que divida al reloj?
Los dos relojes
Ayer comprobé mi reloj de pared y mi despertador y puse sus manecillas en punto. El reloj de pared se atrasa 2 minutos por hora, y el espertador se adelanta 1 minuto también por hora. Hoy se pararon los dos relojes: se les acabó la cuerda. En la esfera del reloj de pared las manecillas marcan las 7 en punto, y en la del despertador, las 8. ¿A qué hora comprobé ayer los relojes?
El enunciado del problema tiene dos objeciones. Una te la diré al final, pero la otra es que está puesto para despistarte, así que vamos a hacer una tabla que nos permita saber qué ocurre con cada reloj:
| Reloj | Marcha | Se paran |
| Pared | -2 | 7:00 |
| Despertador | +1 | 8:00 |
Con esta tabla ya nos aclaramos un poco más. Podemos ver lo siguiente:
- Cada hora, los relojes se separan 3 minutos.
- Al final, cuando se paran los relojes, están separados una hora.
Y ya no necesitamos más. ¿Cuánto tiempo es necesario que pase para conseguir 60 minutos de diferencia? Efectivamente 20 horas.
Y ahora tienes que ver la otra objeción del enunciado del problema del que te hablaba: Si los dos relojes se han parado a la vez, eso significa que hace 20 horas que se les dio cuerda. ¿Pero hay alguien que esté tan atento de sus relojes? Yo creo que lo ideal habría sido enunciarlo como «hoy miré los relojes y uno marcaba las 7:00 y otro las 8:00 ¿cuántas horas han pasado desde que les di cuerda?»

Si quieres contactar conmigo puedes hacerlo aquí
Si te gusta lo que hago y quieres invitarme a un café 
Vida de la entrada:
– 2020-08-10: Publicación.
– 2020-09-02: Corrección erratas. Añadido botón Paypal.
Bibliografía
- Deulofeu, J.; 2018; Relojes, medidas y calendarios: un sinfín de historias matemáticas; Ed. Gedisa; Barcelona; ISBN: 978-84-18193-08-8.
- Perelmann, Y.; Problemas y experimentos recreativos; MIR; Moscú.
problemas-relojes-eso
 No de estos no vamos a hablar. No son estos los problemas de relojes que vamos a estudiar
No de estos no vamos a hablar. No son estos los problemas de relojes que vamos a estudiar Efectivamente de estos son los relojes de los que vamos a hablar. Los problemas de relojes que estudiaremos son aquellos que se pueden plantear en relojes de manecillas
Efectivamente de estos son los relojes de los que vamos a hablar. Los problemas de relojes que estudiaremos son aquellos que se pueden plantear en relojes de manecillas





