▶ 📚 Problemas de proporcionalidad inversa 🙄
Así que le has cogido el gustillo a los problemas de proporcionalidad y te vienes por aquí para saber algo más sobre proporcionalidad inversa ¿no? Pues lamento decirte que estás en el sitio adecuado.
De hecho no sé si ya has leído otras entradas sobre problemas aritméticos, y en especial sobre proporcionalidad directa. Esta última entrada te la recomiendo pues es la anterior a esta.
Los problemas de proporcionalidad directa e inversa, se empiezan a estudiar en 1ESO. Junto a ellos se estudian los repartos proporcionales y la proporcionalidad compuesta aunque esta última se estudia con mayor profundidad en 2ESO. En 3ESO ya te puedes considerar un experto en problemas de proporcionalidad.
¿Qué es la proporcionalidad inversa? 
En esta entrada ya te dije que:

Pero en aquella entrada nos encargamos de las magnitudes directamente proporcionales, así que ahora toca ocuparse de las inversamente proporcionales

Algebraicamente se escribe así: ![]()
La anterior fórmula representa una hipérbola equilátera, pero de eso no nos vamos a ocupar en esta entrada. Lo que sí vamos a hacer es ver cómo es su repreesentación gráfica:

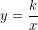 . En este caso concreto
. En este caso concreto 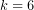 .
.Te cuento cómo he creado la gráfica y lo analizamos.
Cómo he creado la gráfica anterior 
Al igual que hice con la entrada de proporcionalidad directa, te voy a decir cómo he creado la gráfica anterior con el programa R.
datos<-(1:10)
fun<-function(x){6/x}
curve(fun(x), xlim=c(0,7), ylim=c(0,6.5), lwd=2, col="red", main="Función de proporcionalidad inversa")
points(fun(datos)~datos, pch=17, lwd=2, cex=1.5, col="darkgreen")Te analizo qué he hecho en cada línea:
- 1️⃣ En las primera linea creo un vector que va a ser mi variable independiente.
- 2️⃣ La segunda línea está dedicada a crear una función de proporcionalidad inversa.
- 3️⃣ Las dos líneas de código siguiente codifican lo siguiente:
- ✔ Codifica la gráfica a la que añade la función
 . Además se añade el título y los límites de los ejes.
. Además se añade el título y los límites de los ejes. - ✔ Las última línea de código es necesaria para añadir los triangulitos de colores sobre la gráfica.
- ✔ Codifica la gráfica a la que añade la función
Bueno, y ya que te he contado cómo codificar la anterior gráfica, voy a explicarte ahora qué significa.
Cómo interpretar la gráfica 
La gráfica roja 🔴 que ves representada en la figura anterior representa una función de proporcionalidad inversa. ¿Y esto qué significa? Pues ni más ni menos que si multiplicamos ambas magnitudes (variables), su cociente siempre será una constante (en este caso 6). Te lo he puesto en la siguiente gráfica.
| V. independiente ( | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V. dependiente ( | 6 | 3 | 2 | 1.5 | 1.2 | 1 | 0.8571 |
| Producto ( | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
Coloquialmente puedes decir que cuando aumenta una magnitud disminuye la otra en igual proporción 📉. Ten cuidado porque no todas las funciones decrecientes representan proporcionalidad inversa; estoy pensando en una recta de pendiente negativa como ![]() , esta función es decreciente pero no es una función de proporcionalidad inversa.
, esta función es decreciente pero no es una función de proporcionalidad inversa.
Situaciones en las que te puedes encontrar proporcionalidad inversa 
Las situaciones en las que te vas a encontrar problemas de proporcionalidad inversa son aquellos en los que determinada tarea se hace por una serie de personas y te preguntan cuanto tardarían si hubiese más o menos personas trabajando.
A veces no son personas, si no máquinas que están haciendo un trabajo y de repente se añaden algunas o desaparecen algunas o bien conductos que llenan un determinado depósito en un tiempo establecido y de pronto hay más o menos. En general en todos estos problemas te tienes que preguntar algo así como
Puesto que hay más…… ¿se va a tardar más o menos en……?
A continuación te voy a resolver algunos problemas tipo que te puedes encontrar a lo largo de tu etapa escolar.
Problemas tipo de proporcionalidad inversa 💥
1️⃣ Ejemplo 1
Una peonada de 5 albañiles tardan en construir un muro 90 días. Si deben terminar la obra en 15 días, ¿Cuántos albañiles hacen falta?
Lo primero 
| Albañiles | Días | Constante ( | |
| Enunciado | 5 | 90 | |
| Problema | 15 |
Como puedes ver, la columna clave es la que he nombrado como constante que no es otra cosa que la constante de proporcionalidad. En este caso, al ser proporcionalidad inversa, lo que es constante es el producto, así pues, ya tengo planteada la ecuación que debo resolver:
![]()
Y esto que nos ha salido ¿Qué es lo que es? 
Se necesitan 30 albañiles para construir el muro en 15 días.
Y ahora te propongo una pregunta, para que contestes en comentarios si te apetece. ¿Cuántos albañiles hacen falta para construir el muro en 16 días? ⁉
2️⃣ Ejemplo 2
Una cisterna se llena en 9 horas cuando el caudal de entrada es 720 litros cada minuto. ¿Cuánto tardaría en llenarse si entrasen 500 litros cada minuto? ¿y si entrara un metro cúbico cada minuto?
En este problema, antes de empezar a hacer números, debemos darnos cuenta de una cosa: No todas las unidades son las mismas. Es decir, hay un caudal que te lo dan en ![]() , otro caudal te lo dan en
, otro caudal te lo dan en ![]() y el tiempo de llenado te lo dan en
y el tiempo de llenado te lo dan en ![]() .
.
Así que lo primero que debes hacer es arreglar las unidades. Yo lo voy a poner todo en ![]() y en
y en ![]() :
:
![]()
![]()
![]()
Y ahora que tengo todas las unidades bien puestas, es decir, que todas son homogéneas, elaboro mi tabla, teniendo en cuenta que tengo que responder a dos preguntas diferentes:
| Caudal ( | Tiempo ( | Constante ( | |
| Enunciado | |||
| Pregunta A | |||
| Pregunta B |
Y ahora voy a resolver cada una de las preguntas
Pregunta 🅰
En este caso la ecuación a resolver es:
![]()
Pregunta 🅱
Para resolver esta pregunta debemos resolver lo siguiente:
![]()
Soluciones 🧮
Por último tienes que explicar las soluciones que has calculado, ya que si no lo haces, tu profe que no te tiene manía, te lo contará como incorrecto. Y ten cuidado que hemos calculado un tiempo y entonces rige el sistema sexagesimal.
Así tenemos:
- Pregunta A:

- Pregunta B:

3️⃣ Ejemplo 3
Anselmo posee pienso suficiente para alimentar a sus 72 vacas durante 12 días. Mañana le van a traer otras 36 vacas más, ¿Cuánto tiempo podrá alimentarlas con el forraje que tiene?
Este problema es más sencillo que el anterior. Lo único que debes tener en cuenta es que si Anselmo tiene 72 vacas 🐄 y mañana le llegan otras 36; tendrá en total 108 vacas. Como siempre, lo primero es hacer la tabla resumen del problema.
| Vacas | Días | Constante | |
| Enunciado | |||
| Problema |
Ya eres un experto en problemas de proporcionalidad inversa, así qeu espero que resolver éste no sea nada difícil:
![]()
Así la solución es:
Anselmo tendrá pienso para dar de comer a su ganado durante 8 días.
4️⃣ Ejemplo 4
Un equipo de 10 programadores informáticos son capaces de crear un programa en 12 días. Si fueran 12 programadores ¿Cuánto tiempo tardarían?
Supongo que este problema ya no es nada difícil para ti que te has convertido en un experto en proporcionalidad inversa. Vamos con la tabla:
| Programadores | Días | Constante | |
| Enunciado | |||
| Problema |
Este problema es tan sencillo, que no necesitas ni siquiera plantear una ecuación.
Fíjate en la primera constante. Te dice que ![]() y ahora en la que debes calcular, que te dice
y ahora en la que debes calcular, que te dice ![]() ¿Cuánto va a valer tu incógnita? Exacto 10
¿Cuánto va a valer tu incógnita? Exacto 10
Así que con 12 programadores, tardaríamos 10 días en teclear el programa. 💻
🎉 En resumen
Espero que con esta entrada te haya quedado claro qué son los problemas de proporcionalidad inversa y cómo resolverlos. Como has podido comprobar, todo se basa en hacer una tabla e ir colocando los datos que te da el problema. Las ecuaciones que suelen aparecer son muy sencillas, por lo que su resolución no te debe plantear ningún problema.
Si quieres contactar conmigo puedes hacerlo aquí
Si te gusta lo que hago y quieres invitarme a un café 

Bibliografía:
- Colera Jiménez, J., Oliveira González, M. J., Gaztelu Albero, I., Colera Cañas, R.; 2016; Matemáticas orientadas a las enseñanzas académicas: 3 ESO; Ed. Anaya; Madrid; ISBN: 978-84-678-5213-4.
- VV.AA.; 2015; Matemáticas orientadas a las enseñanzas académicas 3ESO; Ed. Santillana – Serie RESUELVE; Madrid; ISBN: 978-84-680-1285-8
Vida de la entrada:
– 2020-11-19: Publicación.
– 2021-05-02: Corrección de un error en el ejemplo 1. ¡¡Gracias Lizeth!!







