▶ 🎖 Teorema de Thales, árboles y la Tierra 📐
El teorema de Thales 📐 es uno de los teoremas más famosos de la geometría. La primera vez que habrás oído hablar de él será en 2 ESO, y te lo volverán a repetir en 3 ESO.
Unas veces verás escrito Tales y otras veces Thales. No sé cuál es la grafía correcta, pero yo lo aprendí con hache, así que escribo Thales. Lo importante es que seas coherente y siempre escribas de la misma manera.
Enunciado y demostración del teorema de Thales
Hay varias formas de enunciar el teorema de Thales, pero yo te doy la siguiente que es la que aparece en el libro de Bruño (1961), y también Buser (2010), aunque en este último, de una manera mucho más compleja :
Teorema de Thales:

Vamos a demostrar este teorema. Es muy sencillo. Fíjate en la siguiente figura:

Vamos a trabajar con el triángulo ![]() , que es el triángulo que está marcado en negrita. La prolongacion de los lados son las rectas dibujadas en azul discontinuo y el resto de segmentos que ves cumplen las hipótesis del enunciado del teorema.
, que es el triángulo que está marcado en negrita. La prolongacion de los lados son las rectas dibujadas en azul discontinuo y el resto de segmentos que ves cumplen las hipótesis del enunciado del teorema.
Fíjate 
![]() que comparte el vértice con el triángulo principal y además el lado
que comparte el vértice con el triángulo principal y además el lado ![]() es paralelo a
es paralelo a ![]() . Vamos a ver que son, efectivamente, semejantes, es decir,
. Vamos a ver que son, efectivamente, semejantes, es decir, ![]() .
.
- El ángulo
 es común para ambos triángulos.
es común para ambos triángulos. - El ángulo
 del triángulo
del triángulo  es igual al ángulo
es igual al ángulo  del triángulo
del triángulo  ; por ser ángulos correspondientes:
; por ser ángulos correspondientes: 
- De la misma manera deducimos que

Los lados de ambos triángulos serán proporcionales de acuerdo al teorema de los segmentos proporcionales; es decir:
![]()
Si ahora nos fijamos en el segmento ![]() , tenemos que:
, tenemos que:
![]()
Como en estas dos igualdades aparece una fracción común, ![]() y además, ocurre que
y además, ocurre que ![]() por ser lados opuestos de un palalelogramo:
por ser lados opuestos de un palalelogramo:
![]()
Por tanto, los triángulos ![]() y
y ![]() tienen sus ángulos respectivamente iguales y sus lados homólogs proporcionales. Esto significa que son semejantes, es decir:
tienen sus ángulos respectivamente iguales y sus lados homólogs proporcionales. Esto significa que son semejantes, es decir:
![]()
A la misma conclusión se llega comparando cualquiera otro de los triángulos que aparecen en el dibujo: ¿Te atreves a dejarlo en comentarios?
A partir de este teorema se puede hablar de los criterios de semejanza de triángulos, pero esto lo dejamos para otra entrada.
Otro teorema de Thales
Si has estado buscando en la wikipedia cuestiones sobre el teorema de Thales, verás que allí te dicen que hay dos teoremas que tienen el apellido de Thales. El segundo teorema es una propiedad de las circunferencias y los triángulos rectángulos (el punto medio de la hipotenusa es el circuncentro), y yo no te voy a hablar de ello en esta entrada, porque, en España al menos, cuando en clase hablamos del teorema de Thales, nos referimos a lo que te he contado hasta el momento y lo que te voy a seguir contando a continuación.
El teorema de Thales en 2 ESO
En 2 ESO, te habrán enseñado el teorema de Thales con un enunciado parecido al siguiente (de hecho, es como lo enuncia Puig Adam (1980)):
Teorema de Thales:

![]() y
y ![]() se cortan por un sistema de paralelas, los segmentos determinados por los puntos de intersección sobre una de ellas son proporcionales a los determinados por los puntos correspondientes sobre la otra
se cortan por un sistema de paralelas, los segmentos determinados por los puntos de intersección sobre una de ellas son proporcionales a los determinados por los puntos correspondientes sobre la otra
Este enunciado es un poco lioso, pero viene a decir que si tienes dos rectas ![]() y
y ![]() (que pueden ser o no ser paralelas) pero sí se cortan con un haz de rectas paralelas, entonces la longitud de los segmentos que aparecen en
(que pueden ser o no ser paralelas) pero sí se cortan con un haz de rectas paralelas, entonces la longitud de los segmentos que aparecen en ![]() son proporcionales a los que aparecen en
son proporcionales a los que aparecen en ![]() .
.
Personalmente no me acaba de convencer esta forma de enunciar el teorema de Thales en la ESO por varias razones:
- Existen tres formas diferentes de dibujar las rectas
 y
y  . En realidad son sólo dos: o son paralelas o son secantes; pero éste último puedes dividirlo en:
. En realidad son sólo dos: o son paralelas o son secantes; pero éste último puedes dividirlo en:- Se cortan en el dibujo que tienes en el papel.
- Se cortan fuera del papel
- Algunos alumnos no se dan cuenta de que los segmentos que son proporcionales son aquellos que se forman sobre las rectas
 y
y  , y no sobre el haz de paralelas.
, y no sobre el haz de paralelas. - La mayoría de los ejercicios que conozco para 2 ESO y 3 ESO (por no decir todos…) se resuelven con triángulos en posición de Thales, que no es más que la figura sobre la que te he demostrado el teorema de Thales antes.
Lo que quiero decir es lo que puedes ver en la siguiente figura. En ella ves las tres posiciones que debes tener en cuenta y es posible que te des cuenta de lo que dice el pie de foto.

 y
y 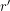 son secantes, y en la tercera son paralelas. Cuando se enseña así el teorema de Thales hay que dejar muy claro que los segmentos proporcionales son los que aparecen en las rectas
son secantes, y en la tercera son paralelas. Cuando se enseña así el teorema de Thales hay que dejar muy claro que los segmentos proporcionales son los que aparecen en las rectas  y
y 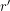 (negras) y NUNCA sobre el haz de paralelas (rojas); muchos alumnos son proclives a equivocarse en este punto.
(negras) y NUNCA sobre el haz de paralelas (rojas); muchos alumnos son proclives a equivocarse en este punto.A partir de enunciar el teorema de esta manera puedes llegar a la figura que te he puesto al principio como un corolario del teorema de Thales:
Corolario del teorema de Thales:

El dibujo en el que se superponen dos triángulos semejantes compartiendo un ángulo, se llama triángulos en posición de Thales.
Ejercicios típicos de 2ESO
A continuación te presento algunos de los ejercicios típicos que se resuelven con el teorema de Thales y
Ejemplo 1: Calcula las longitudes que faltan
Este es un ejercicio típico de clase y de examen. Tu profe, que no te tiene manía, te va a dar una construcción similar a la siguiente y te va a pedir que halles las longitudes que faltan:

Puedes utilizar cualquiera de los dos enunciados que hemos dicho del teorema de Thales. Lo importante es que se cumplen las hipótesis del mismo:
- Existen dos rectas secantes.
- Un haz de rectas paralelas cortan a las anteriores.
De esta manera sabemos que se cumplen las siguientes iguadades:
![]()
¿Y por donde empiezo? por la fracción de la cual conoces su valor numérico:
![]()
Por lo tanto el problema queda reducido a:
![]()
Y sólo queda resolver cada una de las igualdades por separado:
![]()
![]()
![]()
Podrías haber trabajado con triángulos en posición de Thales (lo vamos a hacer en el siguiente problema), así que ten un poco de paciencia.
Truco(s):
- Es muy importante que nombres correctamente los puntos. Yo te he dejado aquí una recta donde todos los puntos son
 y en la otra recta son
y en la otra recta son  .
. - La fracción debe ir en orden: esto quiere decir que los puntos que aparezcan en el numerador deben ser siempre de una de las rectas y los que aparezcan en el denominador deben ser de la otra recta. Tienes que ser coherente.
Ejemplo 2: Calcula los lados que faltan del triángulo.
Este es otro tipo de ejercicio que estoy casi seguro que te caerá en algún examen. Por ejemplo, la torre Eiffel proyecta una sombra de 375 m sobre el campo de Marte, mientras que tú, que mides 1,6 m proyectas una sombra de 2 m. ¿Qué altura tiene el monumento?
El esquema que debes hacerte en la cabeza es el siguiente. Como puedes ver, hay dos triángulos que están en posición de Thales ¿por qué? porque al estar el Sol tan lejos, podemos considerar que los rayos llegan paralelos hasta Paris.

Así pues, tenemos dos triángulos en posición de Thales y por tanto: ![]() y por tanto:
y por tanto:
![]()
Ten en cuenta que en este caso he puesto siempre los lados correspondientes al triángulo mayor, en el numerador.
Ahora vamos a ir poniendo los datos que tenemos. Debes considerar que las longitudes ![]() y
y ![]() , aunque las podemos calcular con Pitágoras, no nos las piden y no las calcularemos:
, aunque las podemos calcular con Pitágoras, no nos las piden y no las calcularemos:
![]()
Y como en dos fracciones que son iguales se cumple aquello de que producto de extremos es igual al producto de medios, tenemos:
![]()
Por tanto, la altura de la torre Eiffel es de ![]()
Ejemplo 3: Localización de números racionales en la recta real
Esta es una aplicación típica, típica del teorema de Thales que tendrás que utilizar en 4 ESO. Te lo dejo todo mucho mejor explicado (con vídeo incluido) en esta entrada, así que no voy a contarte mucho más.
No es más que la aplicación directa de lo que hemos hecho en el Ejemplo 1.
Otras aplicaciones del teorema de Thales
Es muy común oír en clase de matemáticas frases como «y a mí para qué me sirve todo esto», o bien la equivalente «¿y esto para qué sirve?» o algunas similares como «si alguna vez lo necesito ya lo miraré en Google».
La verdad es que es bastante triste oír cosas así, puesto que por la misma razón, ¿para qué sirve cenar si te vas a levantar en ayunas?, o ¿por qué tienes que aprender a leer si hay audiolibros que te recitan el texto? o bien ¿Para qué tengo que aprender a escribir a mano si todo se hace con ordenador? No voy a entrar en esta cuestión, pero en algún lugar leí que, tal y como se están poniendo las cosas, el mayor acto de rebeldía es estudiar.
Te voy a mostrar aquí dos aplicaciones curiosas del teorema de Thales que espero te sorprendan:
Eratóstenes, Thales y la Tierra
¿Sabías que Eratóstenes fue un matemático griego que vivió entre los siglos III y II a.C.? Probablemente lo conozcas por la criba de Eratóstenes que se usa para detectar números primos; y quizá no sepas que fue capaz de medir el radio de la tierra con ayuda de un palo, su sombra y el teorema de Thales. Cometió un error de alrededor del 10%, lo que está muy, pero que muy bien (el error depende de cuánto midiese el estadio que era la unidad de longitud de la época y tenía dos versiones distintas: la de la Magna Grecia y la de Egipto).
Así que ya sabes, hace unos 2200-2300 años, los griegos habían medido el radio de la Tierra y se sabía que era esférica (todo lo esférica que es nuestro planeta, claro…)
¿Cómo lo midió?
Eratóstenes se fijó en que cierto día del año en Alejandría la luz del Sol entraba hasta el fondo de un pozo, mientras que esto no pasaba en Siena (hoy Asuán). Así que se imaginó:
- Que los rayos del Sol eran paralelos (de todas maneras, el Sol está tan lejos que no es nada descabellado suponer esto).
- Sabía la distancia entre Alejandría y Sienna.
- Midió la sombra que proyectaba él mismo o una cayada (hay versiones para todos los gustos, ya sabes lo que ocurre con las leyendas….)
¿Te atreves a hacer tú el esquema? déjalo en comentarios y dinos qué triángulos debes usar para calcularlo….
Medición de árboles
La mejor forma de ver cuán alto es un árbol 

Además, saber la altura de los árboles es el primer paso para saber cuánta madera hay, cuánto están creciendo, etc y eso es la primera fase de cualquier plan de ordenación o sus revisiones (el plan de ordenación de un monte es el documento que establece cómo gestionarlo para conseguir recursos y conservarlo).
Pero no nos desviemos en temas de selvicultura. Existe un hipsómetro (el aparato que se utiliza para medir alturas de árboles) que se llama regla de Christen. Yo me construí una cuando estudiaba selvicultura y es la que puedes ver a continuación:

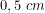 y la fórmula necesaria para hallar la altura de un árbol con un testigo de longitud
y la fórmula necesaria para hallar la altura de un árbol con un testigo de longitud  . En la parte derecha se puede ver la altura del árbol a través de un testigo de longitud
. En la parte derecha se puede ver la altura del árbol a través de un testigo de longitud 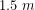 .
. Es necesario darse cuenta que cuanto más alto es el árbol, mayor error se comete en la medición.
Este método no es preciso y se debería usar en las primeras fases de gestión de la masa.
No voy a entrar a contarte las características de la medición con este instrumento, ni sus ventajas ni inconvenientes. Sólo te diré que se basa en triángulos semejantes y el teorema de Thales anda por ahí como puedes ver en el siguiente esquema, y que sí se cometen errores de mediciones que debes tener en cuenta: es decir, si estás gestionando una masa para una clara o un clareo, con árboles menores de 15 m, este instrumento da buenos resultados, o al menos, suficientemente precisos; pero si lo que tienes son árboles de más altura, es mejor utilizar otros métodos, porque vas a cometer grandes errores. Todo es cuestión de cuánto error relativo y absoluto estés dispuesto a asumir.
Además, la función que acaba siendo la base de la medición es una hipérbola, lo cual significa que anda haciendo de las suyas la función exponencial. Si quieres saber algo más de esto puedes pinchar aquí y aquí.
Pero ¿cómo funciona?
Para averiguarlo, ten en cuenta el siguiente esquema:

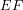 que establece una marca
que establece una marca 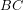 en la regla de Christen. Así se puede saber la altura del árbol
en la regla de Christen. Así se puede saber la altura del árbol 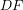 .
Este método tiene mayor error cuanto más alto es el árbol, por lo que se debe usar con cautela en cubicaciones finales. Es muy útil como herramienta de gestión en las primeras etapas de la masa.
.
Este método tiene mayor error cuanto más alto es el árbol, por lo que se debe usar con cautela en cubicaciones finales. Es muy útil como herramienta de gestión en las primeras etapas de la masa.Debes pensar que tenemos dos rectas paralelas y tres rectas secantes:
- Las rectas paralelas son la propria regla de Christen (segmento
 ) y el tronco del árbol (segmento
) y el tronco del árbol (segmento  ). En la parte baja del arbol se sitúa un testigo de longitud conocida (segmento
). En la parte baja del arbol se sitúa un testigo de longitud conocida (segmento  ) que normalmente suele ser de 1,5 m o 2 m.
) que normalmente suele ser de 1,5 m o 2 m. - Las rectas secantes son las que parten del ojo del observador y llegan hasta la base del árbol, el borde superior del testigo y el borde del árbol.
Debes conectar visualmente el extremo de la regla (punto ![]() ) con el vértice del árbol (punto
) con el vértice del árbol (punto ![]() ). En ese momento, el extremo del testigo (punto
). En ese momento, el extremo del testigo (punto ![]() ) te marcará una señal en la regla (punto
) te marcará una señal en la regla (punto ![]() ) y trabajando con los triángulos que aparecen en la figura puedes llegar a saber la altura del árbol. ¿Te atreves a dejar la respuesta en comentarios?
) y trabajando con los triángulos que aparecen en la figura puedes llegar a saber la altura del árbol. ¿Te atreves a dejar la respuesta en comentarios?
Como ya te he dicho para el final de turno de corta se deben emplear otras maneras más precisas de calcular la altura de un árbol, principalmente aquellas basadas en trigonometría (el turno de corta significa precisamente eso, ¿a que edad se corta un árbol? y varía mucho en años: por ejemplo, para el pino de Monterrey [Pinus radiata] o algunos chopos [Populus spp.] está sobre los 15-20 años, pero para el pino de Valsaín [Pinus sylvestris] puede irse hasta los 120 años o más).
Y hasta aquí la entrada de hoy, si quieres estar al loro 
Si quieres contactar conmigo puedes hacerlo aquí
Si te gusta lo que hago y quieres invitarme a un café 

Bibliografía
- Bruño, G. M.; 1961; Curso de geometría superior; Ed. Bruño; Madrid; Depósito legal: M-4937-1961.
- Buser, P., Costa, A. F.; 2010; Curso de geometría básica; Ed. Sanz y Torres; Madrid; ISBN: 978-84-92948-34-5.
- Puig Adam, P.; 1980; Curso de geometría métrica (2 tomos); Ed. Gómez Puig; ISBN: 8485731-03-4.
- Figuras del árbol y del observador tomadas de https://www.pngwing.com/
Vida de la entrada:
– 2021-01-14: Publicación.
–







